Systematic error in the energy calculation neglecting 2nd order terms in
the calculation of dL

Purpose of this analysis is to estimate the systematic error on the 1st order
calculation of dL, neglecting the higher order terms of the beam displacement.
This is done in one particular case: considering the reference orbit as the
central orbit. This is the case that one wants to study because, in the general
case, one has to consider the variation of the displacement of the reference
orbit along s (position around the ring). This quantity is difficult to measure
in practice because the BPM system is not "absolutly" calibrated.
Considering the central orbit as reference orbit, it is possible to exactly
calculate the orbit length for a general orbit as
L = cyclic int (sqrt ( f(s) ) ) ds , where
f(s) = (1+X/ro)^2 + (dX/ds)^2 (for bent sections) and
f(s) = 1 + (dX/ds)^2 (for straight sections)
(X: beam displacement at the position s, with respect to the reference orbit;
ro: average bending radius of the bent sections)
Because the reference orbit is the central orbit, it is NOT possible to use
this "exact" calculation to get physical results. ALL OF THIS IS A TEST OF THE
1st ORDER ALGORITHM TO CALCULATE dL.
It has been compared the "exact" dL with the 1st ord. dL for the stable run
run stack res
704 3 chi2
706 3 chi2
707 3 chi2
708 3 chi2
709 3 chi2
839 6 psip
1011 8 psip
1313 19 1p1
1314 19 1p1
1315 19 1p1
1424 21 chi1
1425 21 chi1
1431 21 chi1
2015 22 psip
2202 38 chi2
2218 39 psip
2399 50 1p1
2421 52 1p1
2422 52 1p1
2440 54 1p1
2450 55 1p1
2451 55 1p1
2452 55 1p1
3014 56 1p1
3022 57 1p1
3023 57 1p1
3025 57 1p1
3026 57 1p1
3047 58 1p1
3050 58 1p1
3079 60 jpsi
3091 61 1p1
3092 61 1p1
3149 63 1p1
3150 63 1p1
3151 63 1p1
3194 65 chi1
3288 74 chi1
in three different configurations of BPM saturation:
The results are summarized in this plot:
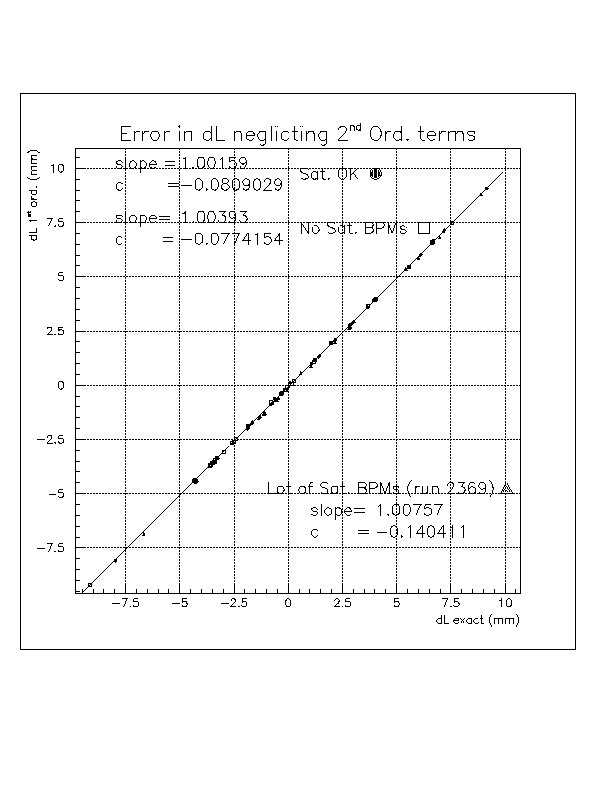
In average, the 1st order dL understimate the "real" dL for 80 um
(Sat. OK value). Furthermore, the error slightly depend upon dL: in the case
of Sat. OK (slope = 1.002), this means that the 1st order calculation of
dL = 10 mm is underestimated by 60 um and of dL = -10 mm by 100 um.
This is an error of /e835/people/15 KeV in energy in the worst case.
These are the table of data:
correct saturation pattern for the given run
BPMs considered NOT saturated
BPMs considered saturated like in run 2369

Last update of this page -- Tue Mar 3 15:10:50 CST 1998
useful links:
 E835 Home Page
E835 Home Page
E835 run info table: alphanumerical ;
only numerical (useful for paw)
Offline energy calculation stack per stack
Golden Data Stream and DSTs Page
Luminosity Home Page
ACNET run number stack per stack
BPM saturation history
Single Value Decomposition Threshold Plots
Beam Position and Angle at the target from BPMs
Systematic error in the energy calculation neglecting 2nd order terms in the calculation of dL
BPM position vs time stack per stack
Maintained by Gabriele Garzoglio.
Comments, problems or questions -- please send
mail.
